Mortgage Math

Wonkish Details

Jump to the Results section directly if you're not interested in the theory.

Amortization formulas

The formulas for amortization are as follows (see here for detailed derivation). If we have a mortage with principal $P$, monthly interest rate $r$, and term $n$, then the monthly payment, $A$, is given by $$A = P\left[{r\left(1+r\right)^n\over \left(1+r\right)^n-1}\right]\tag{2}$$ The interest accumulated in the $m^{th}$ period (and, consequently, the interest portion of the $m^{th}$ payment) is $$I_m = r p_{m-1}, \tag{4}$$ which is the tax-deductible portion.

Inflation, Long-Term Bond Yields, and the Discount Rate

Now we factor in the discount rate. This is essentially the time-value of money, and is usually a function of some essentially risk-free investment (e.g., 30-year Treasury Bonds) and your own personal pet variables such as the rate of inflation.

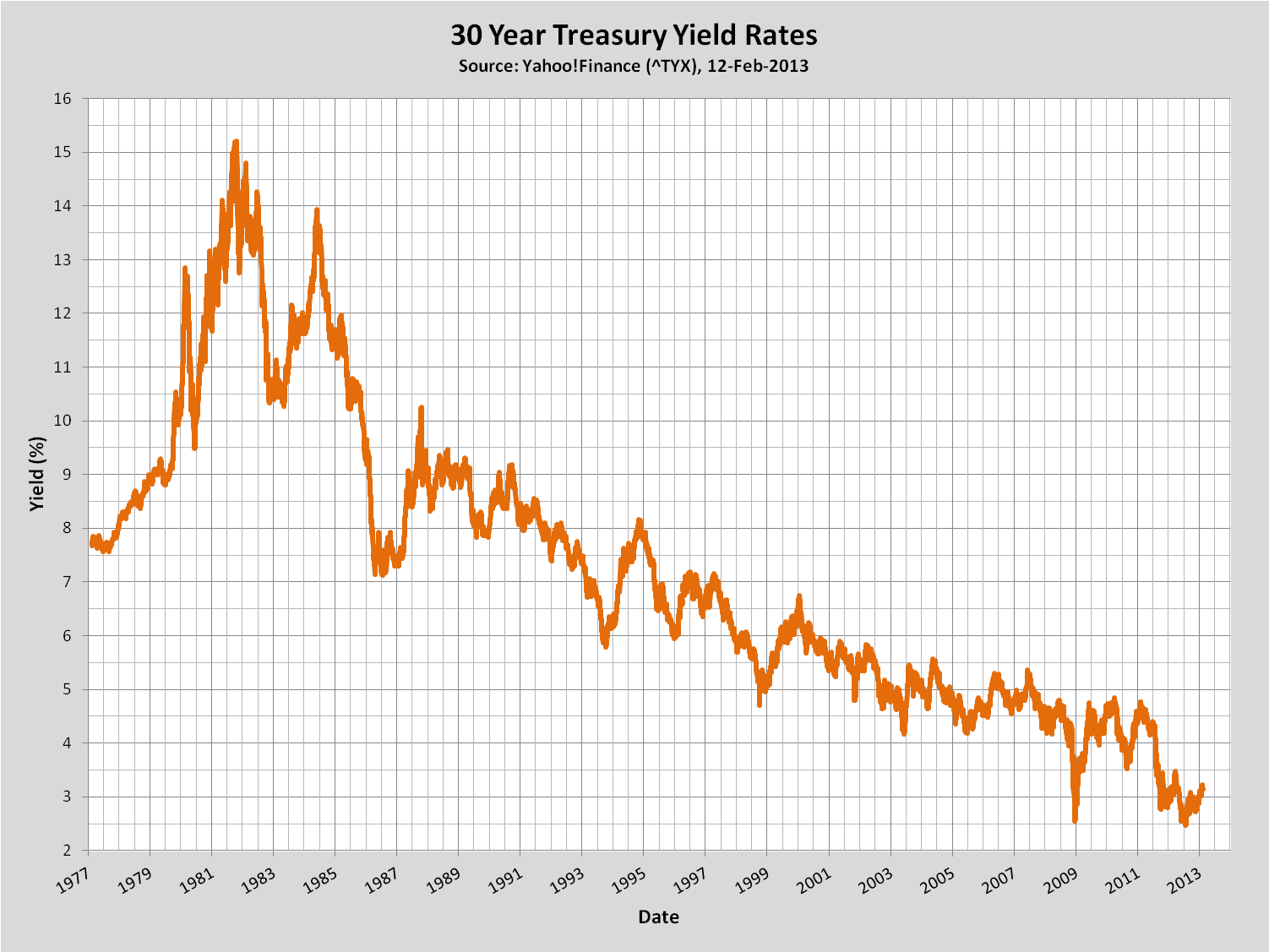
See below for a plots of historical data of inflation rates and long-term yields (click on a figure to see a larger version).

Results

There are two things of interest

Is it worth paying points and closing costs? What's the break-even point taking taxes, etc., into account
Should you prepay? To calculate the NPV you have to make some assumptions about discount rate, so there's some judgment involved. But you can do "what-if".

Marginal Tax Rate Max. Discount Rate Term Scenario A Principal Yearly Interest Rate Points Closing Costs	% % years $ % % $		Figure 1. Monthly Payments	Figure 2. NPV of Cumulative Payments

Scenario B Principal Yearly Interest Rate Points Closing Costs	$ % % $	Figure 3. Break-even analysis of the two scenarios

Notes:

Only equal-term loans are compared. To compare different terms (e.g., 15-year and 30-year) run the calculations separately. A future version may include comparison of different terms, but Figur 3 doesn't make sense in this case.
Assume that closing costs are tax-deductible. Non-deductible closing costs will be included in a future rev.